Machine learning has exploded as companies find ways to draw actionable insights from the data which consumers feed them. However, the efficacy of artificial intelligence algorithms is dependent on the size of the data pool- giving big companies like Facebook and Google a formidable advantage over small scrappy startups. What if we could share data between organizations, to draw insights that are bigger than a single company’s dataset?
There are two ways to enable this: share the data with a (trusted) central entity who runs the computations and returns the estimand, or create consensus between the parties. The first approach requires that the aggregator is trusted to safeguard and properly analyze the data without breaking confidentiality of users; the second requires that each party trust the others.
The first option isn’t feasible under most data use agreements, and may be subject to significant GDPR concerns. The second has been fraught with trust and cybersecurity issues, specifically:
- Trusting that counterparties aren’t intentionally distorting their updates (addressed by my previous paper on cybersecurity in distributed optimization)
- Trusting that counterparties have appropriately computed the optimal update (this post)
- Trusting that the counterparties haven’t falsified data (future work)
- Preserving privacy while computing updates (future work)
Mathematical background
This discusses an architecture for proving that an update in a decentralized optimization algorithm accurately reflects the optimum.
We consider convex optimization problems, for which the guarantees of duality mean that we can create a certificate of optimality. This is a mathematically simple guarantee that a proposed solution is optimal- this is important because it is computationally simple to check, and doesn’t require replicating the optimization algorithm. In the machine learning framework we’re considering, a valid certificate means that the proposed solution accurately represents the actual dataset.
To prove that we have a valid certificate, we’ll use a zero-knowledge proof to prove that the certificate satisfies the optimality conditions, without yielding any information on our dataset.
Architecture
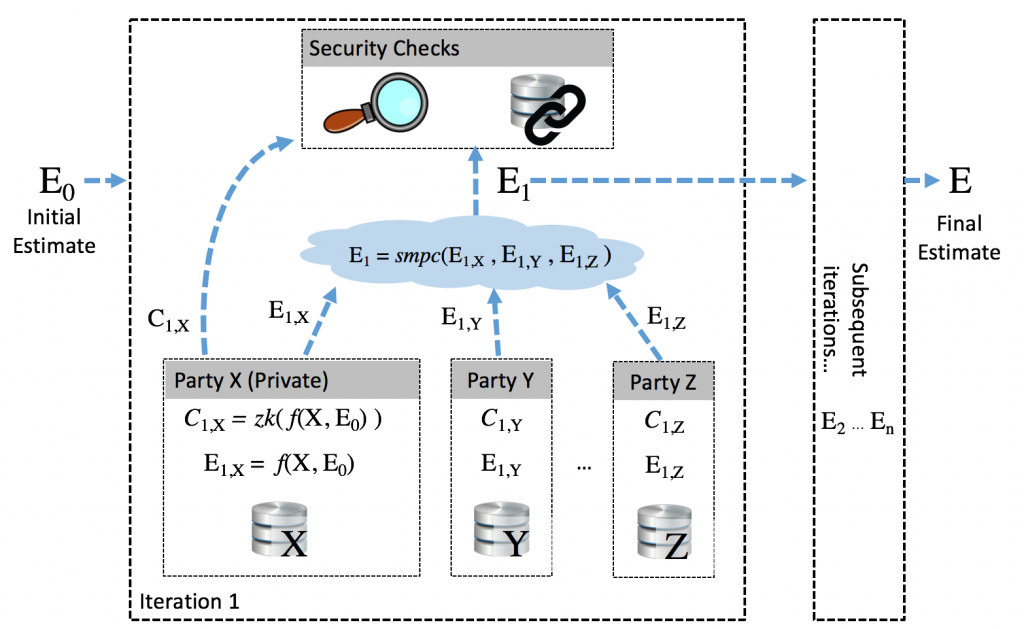
This new architecture looks like this:
- An initial estimate E0 is fed into the system; the goal of each iteration is to update this estimate using private knowledge in order to arrive at the optimal solution E
- Given the initial estimate E0 and its private data (X, Y, or Z), each counterparty computes the solution E1,X= f(X, E0), using conventional decentralized computation techniques.
- They then create a zero-knowledge proof C = zk(f) that the proposed update satisfies the optimality conditions- creating a certificate of optimality which can be shared without revealing any data.
- The parties then combine their updates using secure multi-party computation, allowing the estimate to be updated without revealing anything about individual updates. The zero-knowledge proofs are meanwhile published, allowing each update to be verified.
- Additional security checks can be built into this step, protecting against false data injection, or using blockchains to create an auditable track to verify the computation result.
This concludes one iteration of the decentralized consensus algorithm, and the estimator is now one step closer to optimality. The aggregator (or individual parties, in a fully-decentralized algorithm) can assess the convergence criteria, and repeat the process or end the updates.
The output is guaranteed to be accurate, verifiable, and completely privacy-preserving. This is a far step beyond current privacy-preserving machine learning algorithms, which incrementally leak data, aren’t anonymized, and aren’t trustless.