Conventional centralized optimization algorithms have challenge solving big optimization problems- at some scale, you simply can’t fit the problem on a single computer, let alone manage all of the variables. To solve this, researchers use decentralized optimization techniques to break the problem into a set of subproblems which can be rapidly solved on distributed computers or smart devices- but this exposes the optimization algorithm to cybersecurity threats from hacking these consumer-level devices.
As we rely on decentralized computing to solve more important problems –say, scheduling our electricity grid- these cybersecurity threats will become more important. I’ve been working on methods for securing optimization algorithms, both with blockchains and now with a new paper on the generalized cybersecurity vulnerabilities of decentralized algorithms (see my earlier paper on blockchain-coordinated microgrids).
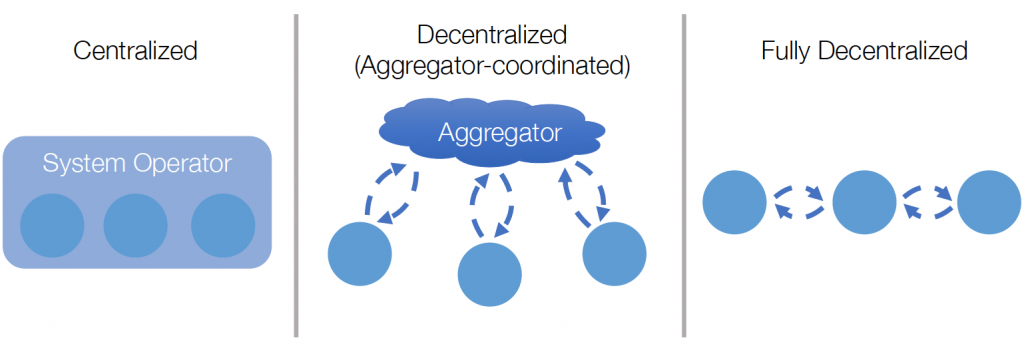
Different structures for solving mathematical optimization problems, from left: Centralized optimization, where all details of objective and constraints are held by a central entity. Decentralized optimization (also called aggregator-coordinated optimization) where local nodes hold local objective and constraint information, and an aggregator brings nodes into consensus on shared constraints. Fully-decentralized optimization, where no centralized entity exists but neighbors communicate directly with each other to achieve consensus.
Our new paper outlines a number of cybersecurity threats to decentralized optimization algorithms which an attacker could exploit, and ways of addressing each:
- Sub-optimal solution: If an attacker can manipulate private information (pose false data, shift private constraints) the other participants will reach consensus on a sub-optimal solution. As this is dependent on private information, there is no way to directly detect this- but it can be minimized by using a statistically-based fault detection model or structuring incentives that discourage lying.
- Infeasible Constraints: An attacker can cause the algorithm to fail by sending infeasible messages- updates which don’t satisfy some publicly known constraint. This can be mitigated by projecting the attack back onto a known set of constraints, as shown in the figure.
- Non-Convergence: When an attacker injects noise into the system, the attack is not easily identified or mitigated with conventional tools: this can look like the outcome of an ill-formed problem, but can cause the algorithm to stall. This paper uses convergence guarantees of the Alternating Direction Method of Multipliers to create a unique detection mechanism that can correctly identifies attacks in 98% of the problems we tested.
To model the effectiveness of our defenses, we simulated over 1000 random Quadratic Programs, a common type of optimization problem which can be used to model regression algorithms, support vector machines, and market clearing problems. Half of these were attacked, and half were unattacked.
Without defenses, attackers were able to bring these optimization algorithms to a standstill – or push them into an infeasible domain, without the coordinator knowing that there is an issue.
By contrast, our detection algorithm correctly identified over 99% of attacks, and we can further improve that metric with additional tuning. The algorithm also doesn’t require much additional computational overhead relative to the underlying problem- and this overhead can be reduced by changing the frequency with which the detection algorithm is run.
The most exciting part of this? It should also work for fully-decentralized algorithms, where there is no central coordinating node. This not only means that it can be applied to a wider variety of problems, but also can be combined with blockchains to secure trustless decentralized optimization problems.