This post describes Problemsolver, a pipeline for improving nonconvex optimization methods by using a large language model to generate novel meta-heuristic optimizers. Nonconvex optimization problems have many local minima and saddle points, making them hard to solve with analytical, interior-point, and gradient-based optimization methods- but may important real-world problems (including the optimization of deep learning model parameters) are fundamentally nonconvex. Inspired by the AlphaEvolve work by Deepmind and using insights from research into creativity, we develop a robust pipeline for rapidly generating, tuning, and testing nonconvex optimization algorithms, in a way which can be extended into other problems and fields.
tl;dr: It worked! Using a robust pipeline for generating new optimizers based on naturally occurring systems we found that over 10% of generated optimizer ideas advanced the pareto frontier of speed and accuracy for metaheuristic optimization techniques. Reasoning models significantly outperformed non-reasoning models, and adding an “evolutionary gene pool” of existing performant code resulted in further performance improvements.
Code is available at https://github.com/emunsing/problemsolver
Context
Many problems can be framed as a maximization or minimization problem, for which an optimization algorithm can be deployed to find a solution to the problem. A few problems may be analytically solvable, some problems can be framed as convex optimization problems which can be solved very efficiently, but many problems are nonconvex. This means that diverging gradients, saddle points, multiple local minima, and sharp discontinuities make optimization hard.
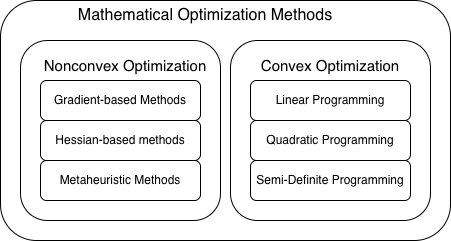
While the reader may be familiar with gradient-based mathematical optimization in modern machine learning algorithms, it’s also worth remembering that many naturally occurring systems -from species evolution to market pricing to language transmission- can also be viewed as an optimization method, in which iterative use of simple heuristics often find good solutions to hard problems. These naturally emergent systems use a mix of exploration and exploitation, local and global message-passing, and individual and group memory to achieve solutions to challenging problems. This observation has led to the field of meta-heuristic optimization to describe a wide variety of algorithms which use heuristic behavior or naturally inspired systems to solve challenging problems through use of mathematically simple methods. Many of these are surprisingly robust, scalable, and adaptable to a wide variety of input problems. A partial list of meta-heuristic algorithms can be found here, and the publication dates of these algorithms are shown below.

Parallels with current ML Optimizers
Metaheuristic algorithms are particularly appropriate for nonconvex and nonlinear optimization problems: because there is no analytically “correct” optimizer, new optimizer systems often leverage heuristic approaches to improving performance, and there can be parallels between mathematically-derived and bio-inspired metaheuristic algorithms. Stochastic gradient descent can be thought of as a way of balancing exploration and exploitation, a momentum term is used in both the Adam optimizer and in many meta-heuristic algorithms, and the use of techniques such as gradient clipping, learning rate schedulers, and higher-order moments and norms can be thought of as heuristic attempts at modulating behavior of optimizers. As we see relatively slow development in conventional machine learning optimizers (Adam was introduced in 2014), it seems promising to revisit lessons from other nonconvex optimizers.
Use of Large Language Models for algorithm improvement
The idea of “recursive self improvement”, i.e. using Large Language Models (LLMs) for improving machine learning algorithms, is not new but has been only recently used effectively- the AlphaEvolve research by Google Deepmind being an important recent example. In that work, LLMs were used to write code for a carefully-scoped problem with a mathematically verifiable solution and a clear fitness metric (e.g. computation cost). The current research builds on this prior work, but with the more ambitious goal of improving the full optimizer, while still using a well-constrained, verifiable problem with strong guards to prevent overfitting and encourage generalizability.
Setup
Test Functions
Existing literature has explored the optimization space of neural nets and large language models [cite], finding that there can be regions of extreme steepness/roughness, many saddle points and local minima, and curved canyons. We choose a set of nonconvex optimization test functions which have these characteristics, and which can be parameterized in an arbitrary number of dimensions while still allowing us to know the true optimum of the problem and assess the true error of the algorithm’s identified solution.
| Function | 2-D Visualization |
| Rastrigin |  |
| Rosenbrock | 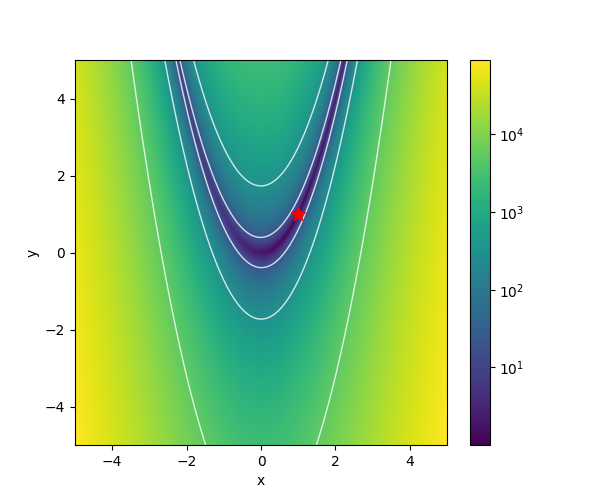 |
| Griewank | 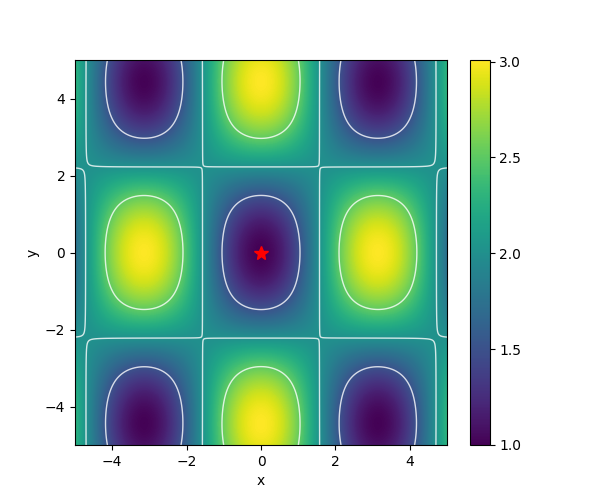 |
| Styblinkski-Tang | 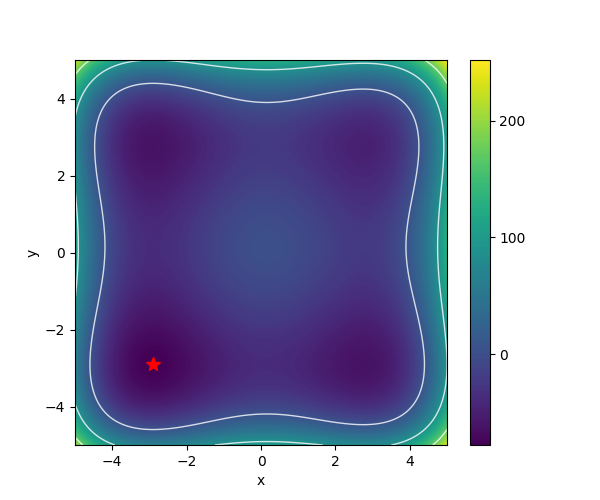 |
| Modified Keane’s Bump | 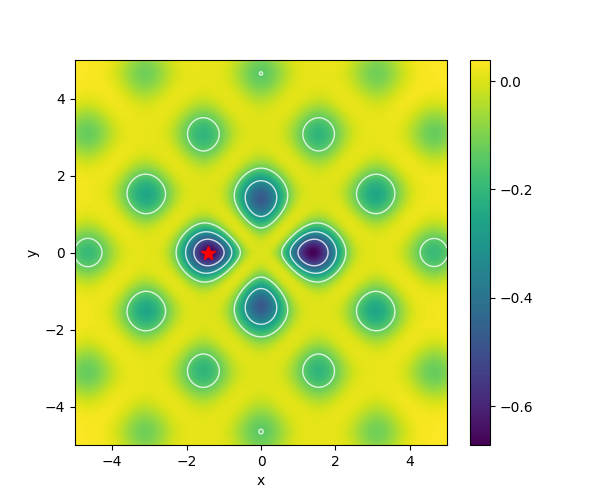 |
Note: We adjust the Keane Bump Function, which is typically symmetric about the x=-y plane, to add a slight paraboloid which biases the solution to the negative of the two original optima.
A future extension would be to use the CEC2017 test functions, which offer a similar set of generalizable test functions, and are commonly used as a test set for nonconvex optimizers.
To prevent overfitting to the set of test problems, we construct a pipeline for generating transformed test functions through use of the variable change operation $x = A^T (z-b)$, parameterized by the matrix $A$ and vector $b$. The transformation matrix $A$ is constructed by taking the QR decomposition of a random normal matrix, then scaling each transformation dimension by a value in the range [0.5, 2]. This results in a skew as well as a scaling/rotation. The simple transformation matrix b then shifts the coordinate system by a random vector drawn in the range [-5.0, 5.0]. The combination of these transformations with the base functions allow us to know the optimal value must lie in the hypercube with bounds [-10, 10].
By creating a standard pipeline for generating new test functions, we are able to guarantee that our training data and test data are always novel, allowing us to scale to arbitrary problem size while preventing overfitting. For each optimizer or hyperparameter evaluation, we draw dozens of instances of translated and reshaped test functions from the distributions above.
We also run the pipeline without access to scipy or pytorch, preventing the generated methods from making a direct call to a solver like L-BFGS or Adam.
Generative optimizer creation
The language model is prompted to generate an optimization function with a function signature like the following:
def minimize(
fun: Callable[[np.ndarray], float],
initial_guess: np.ndarray,
n_estimators: Annotated[int, Interval(low=20, high=200, step=10, log=False)] = 50,
learning_rate: Annotated[float, Interval(low=0.01, high=1.0, log=True)] = 0.1,
alpha: Annotated[float, Interval(low=0.1, high=0.9, step=0.05, log=False)] = 0.5,
rtol: float = 1e-6,
) -> np.ndarray:At runtime, the optimizer will be passed a test function fun that can be called by the optimizer to generate a function evaluation, allowing us to cleanly separate the generated optimization method from the externally provided test functions.
Hyperparameter Optimization and Avoiding Overfitting
To allow fair comparison of different optimization methods, and to avoid comparing multiple optimization methods that differ only in their hyperparameters, we run a hyperparameter optimization method after the optimization function has been generated. In the prompt to the LLM, we explain that the LLM should not focus on guessing good hyperparameters but rather explain that hyperparameters will be optimized with a given budget and ask the model to use Annotated[dtype, Interval(low:float|int, high: for annotating any parameters which are appropriate for hyperparameter optimization. Critically, this relies on the model to reason about which parameters are most significant, and represents a tradeoff between the budget for tuning hyperparameters and the budget for running the optimization.float|int, step: float|int, log:bool)
We build a hyperparameter optimization loop using these settings, and begin the hyperparameter optimization using a set of dozens of randomly-generated transformations of each of the test function above. Because of the potential for extremely time-consuming parameter optimization if the initial parameters are grossly off, we set a maximum time budget for each optimization step and stop the experiment if the elapsed time for the average function evaluation is greater than a threshold.
Performance evaluation
Hyperparameter optimization implicitly requires a univariate loss metric. In this work, we choose to evaluate two metrics: wall-clock execution time, and average absolute log10 relative error. For both metrics, we take the average across a large number of test functions, and to put them on similar scales we multiply the wall-clock execution time by 100 before adding it to the relative error. This performance metric will be used throughout when a univariate performance metric is reported.
When testing multivariate performance, we consider whether the function advances the pareto frontier of existing optimizers: does the proposed code meet or beat the computation speed of all optimizers which offer the same accuracy? Optimizers that meet this pareto-improving criteria are considered “performant” and their code is preserved for future use.
Validation
Because of the large number of potential failure modes for LLM-generated code, we create a test cycle which has multiple checks of the LLM-generated optimizer function. We also run the code in a multiprocessing thread to be able to safely kill it if it takes longer than expected (e.g. if it contains infinite recursion/loop):
- Inspect raw code text for required function signature and annotations
- Check that the optimizer can run for a single test function
- Check that the returned result is the appropriate shape and is bounded
- Run hyperparameter optimization on a randomly generated training set of functions, checking for timeout errors
- Run final validation on a randomly generated test set of functions, checking whether the function meets performance requirements
At each stage, if the function fails a validation we collect error information and feed the error information and the previously generated code back into the prompt for a subsequent attempt.
If the function passes functional tests but does not create a pareto improvement in performance, we also include performance diagnostics in the prompt for a subsequent attempt at creating a more performant optimizer.
Prompting Creativity
Building on the tradition of metaheuristic optimization methods drawing inspiration from emergent phenomena in nature and society, we provide inspiration prompts to the language model to ask it to develop an optimizer which takes advantage of how a specific phenomena demonstrates emergent or loss-minimizing behavior.
To generate a set of potential prompts, we initially asked ChatGPT to write a list of 125 emergent phenomena in nature, society, and physics, along with a 2-3 sentence description of how the phenomena demonstrates dynamics which minimize loss. The inspiration prompts are listed here.
For each phenomena, we ask the language model to use the inspiration in one of two ways:
- Isolated inspiration: We ask the language model to consider the emergent behavior, and develop an optimizer inspired by the behavior.
- Evolutionary approach mixing of divergent approaches: We ask the language model to consider the emergent behavior, and also two code examples of “performant” algorithms which are on our Pareto frontier.
Both approaches benefit from the inspiration phenomena in the following way:
- This creates novelty and variance, increasing the likelihood of a random discovery, novel approach to problem-solving, or the creation of an optimization method which was not seen in the model’s training data
- Existing creativity research has long suggested that genuine creativity may be the result of insights which bridge aspects of two disparate ideas. This “cross-polination” also memetically mirrors the evolutionary approach taken in AlphaEvolve,
In addition, the evolutionary approach benefits from keeping a repository of performant code. This could reduce the likelihood of generating low-quality code, but also may reduce the total diversity of generated approaches by prompting the LLM to be closer to the given examples, resulting in less total diversity.
Implementation Pseudocode
Based on this, we can describe the full optimization approach in the following pseudocode:
for each inspiration in list:
prompt = get_prompt(inspiration)
for improvement_attempt in n_allowed_pareto_improvement_attempts:
train_funcs, test_funcs = generate_transformed_funcs(test_function_set)
for generation_attempt in n_allowed_debug_attempts:
optimizer_fun = llm.invoke(prompt)
try:
validate_optimizer(optimizer_fun)
optimal_params = hyperparameter_opt(optimizer_fun, train_funcs)
break
except:
prompt = prompt_with_feedback(prompt, optimizer_fun, error_msg)
continue
if optimal_params:
performance = benchmark(optimizer_fun, optimal_params, test_funcs)
if is_pareto_improvement(performance):
break
else:
prompt = prompt_with_feedback(prompt, performance)Results
We considered four different models available at the time of the research: GPT o4-mini, GPT-4.1, gpt-oss-120b, and deepseek v3.1.
We create a performance baseline by using the pipeline above to generate optimizers based on the descriptions of seven common optimization algorithms (e.g. Particle Swarm Optimization or PSO) which are well-represented in literature and open-source codebases on which the LLMs were trained. While not a comprehensive set of algorithms, these provide a baseline against which other models will be evaluated and whose code will seed the evolutionary pool.
For each language model model, we run both the baseline (simple inspiration prompt) and the approach which adds two previously discovered performant code samples (called “blend2” here). Due to the high cost of running the o4-mini reasoning model (about $60 to run the experiment here), we did not run o4-mini on the blend2 approach (if anyone at OpenAI wants to hire me or give me API credits, reach out 😉).
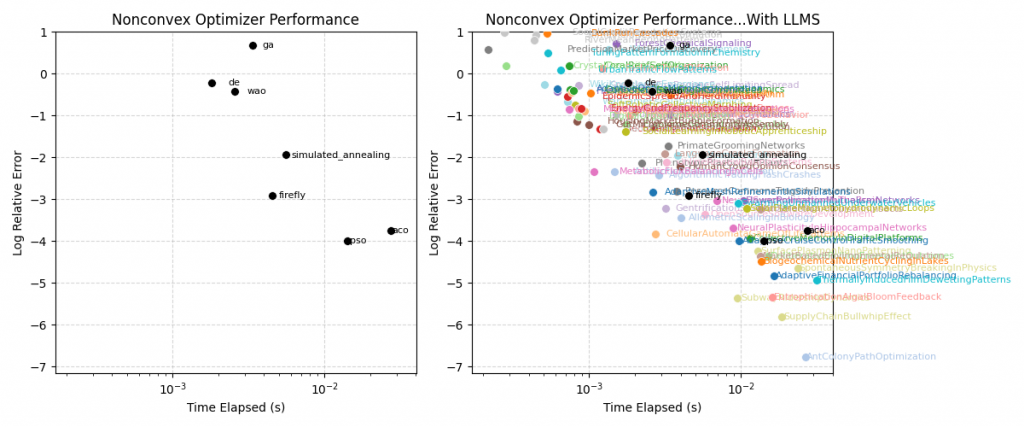
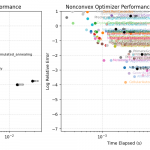
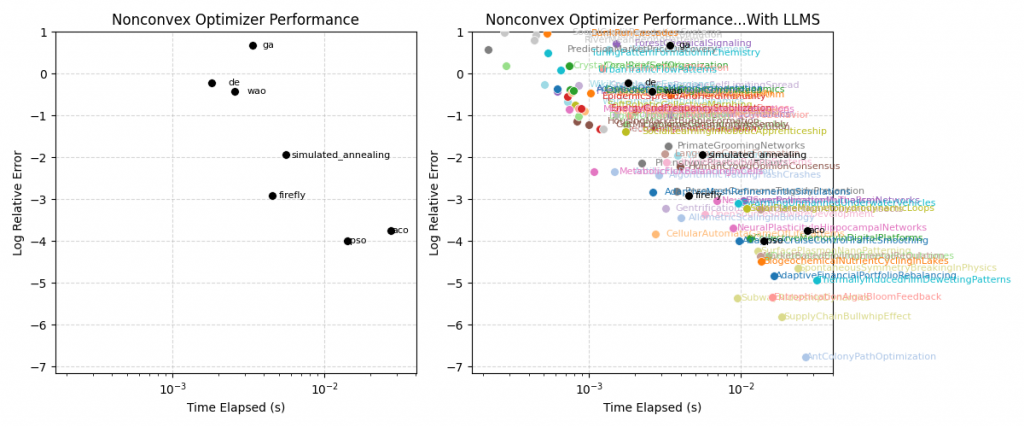
In the plot above, we see the performance of the reference algorithms, and the plot of the performance of all the algorithms generated by the gpt-oss-120b model which advanced that pareto frontier. A more comprehensive set of reference models could be used to provide a stronger guarantee that we are indeed advancing the frontier of knowledge.
Table 1 below shows the summary statistics for each experiment using the simple-inspiration approach. In this table, the pareto pass rate indicates the rate at which attempts exceed the initial pareto frontier, in order to remove path dependence.
| Model | Total # attempts | Pareto pass rate |
| gpt-4.1 | 642 | 13% |
| deepseek v3.1 | 386 | 14% |
| gpt-oss-120b | 393 | 19% |
| o4-mini | 625 | 51% |
We can see the distribution of total loss (log relative error + 100 * compute time in seconds) in the split violin plot below (each side can be viewed as a vertically-oriented histogram). A few observations immediately spring out:
- The blend-2 approach does not offer a dramatic shift in performance: for Deepseek, the performance actually may be better with the baseline model. This is explored below.
- The high pareto pass rate of the o4-mini model does not come across in the total performance metric. Inspection shows that o4-mini produced more successful models in the center and upper-left edge of the pareto curve, which do not translate well into the univariate loss metric. GPT-oss-120b produced results that were more evenly distributed across the pareto curve.
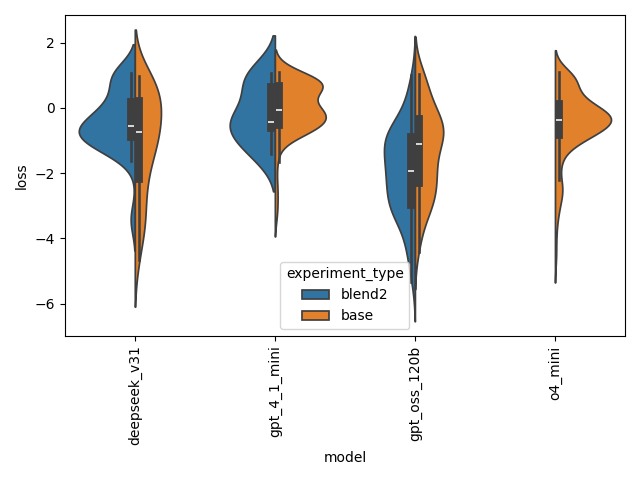
To test whether the blend-2 method is meaningfully better than the simple-inspiration approach, we ran a one-sided t-test to test for improvement. Taken across all models, we believe that there is a difference in means, at the 5% confidence level (p-value: 0.002). However, this is driven primarily by the outsize success of the gpt-oss-120b experiment: When testing sub-populations, we do not see a significant difference in means (deepseek blend-2 mean is not greater than the baseline, and gpt-4.1 was rejected based on the p-value, likely partly due to the small sample size).
To better understand the distribution of results for each model, we can also examine the CDF of the univariate performance metric, which is helpful for identifying the individual contributions to the histograms which are presented as smoothed curves in the violin plots.
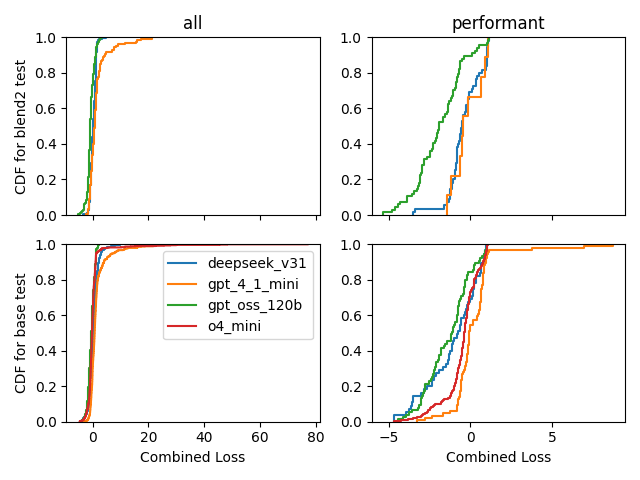
Does Retrying help?
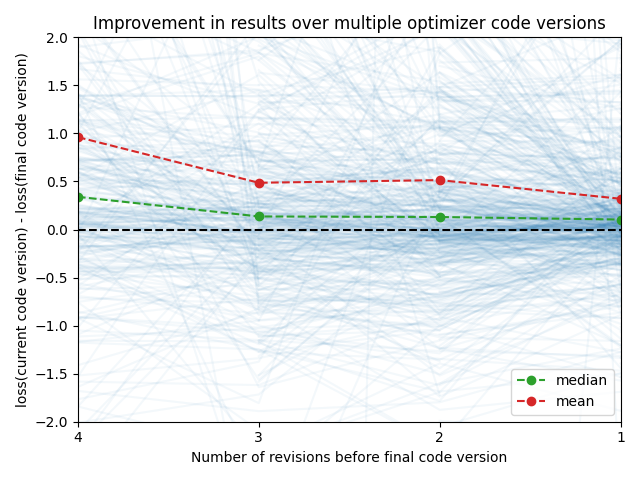
A significant amount of engineering effort went into creating a loop in which the metrics and code of a non-passing attempt is fed back to the LLM prompt for a subsequent attempt at producing a pareto-advancing optimizer. Because we can take up to 5 attempts to produce a successful optimizer, it would be helpful to know if we are gaining much benefit from this, whether we are cycling between equal-valued attempts, or we are seeing a final “a-ha!” moment after multiple attempts which do not succeed.
We see a small but consistent improvement in the loss value over each attempt, when considering the change in loss value from the first attempt (4 attempts away from the final) to the final attempt.
Examining the Efficacy of Evolution
A supposition of AlphaEvolve and similar efforts is that keeping a “gene pool” of successful templates results in gradual improvement over time. In our process, we have to experimental components: the “gene pool” and the “inspiration prompt”. We would ideally like to see a continually decreasing loss in our gene pool (suggesting that we could let the pipeline run for a long time and have a very powerful optimizer).
In practice, the results are not so clear, as seen in the plots below:

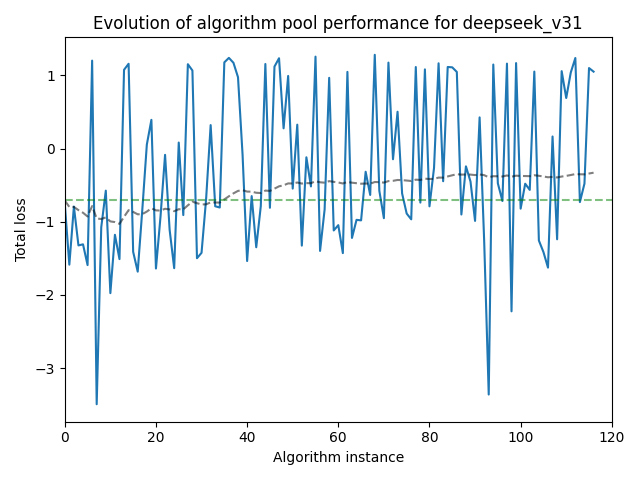
We see a small but continual improvement in the performance of the gpt-oss-120b model over “generations” or algorithm instances, whereas the loss of the deepseek model actually increases over generations.
It is important to note that there is a fundamental tradeoff here: Only keeping the best performers improves the average loss of the pool, but also limits the size of the gene pool and thus the potential for high-variance cross-polination in future generations.
Part of this may be path dependence: Getting a few bad results early in the process can “spoil” the gene pool, leading to poor performance down the line (we do not currently clean less-performant instances out of the gene pool as generations advance).
In our blend-2 experiments, we kept the code from all sample instances which were within 30% of one dimension of the closest point on the pareto frontier. This relative tolerance is a pipeline hyperparameter which could be
Limitations
General limitations with the framework and analysis:
- We have not done a rigorous study on the stability of the test metrics (log relative error, computation speed), which would affect both our hyperparameter optimization and the final metrics which we report on both baseline and generated optimizer performance.
- In practice, we only considered the (simple) 2-D optimization case to reduce the computational time needed to converge on a solution. We do not have a guarantee that the performance of the generated methods extend to higher dimensions.
- A broader set of test problems could benefit the extensibility of the approach, including the CEC2017 test suite or similar.
- For budget reasons, we mostly work with open-source models and excluded o4-mini from the blend-2 task due to high costs. The performance of o4 is clearly a huge improvement relative to many optimizers on this task, and it should be further explored if budget allowed.
Future Work
We are working on extending this approach to gradient-based methods, with the intent of being able to advance the speed and convergence os the optimizers used in neural network optimization.
Conclusions
This work introduces a novel pipeline for generating, tuning, and validating novel metaheuristic optimization methods for nonconvex problems. We introduce a method for preventing overfitting by generating arbitrary nonconvex test functions on the fly, and using these unique function instances in both hyperparameter optimization and in performance benchmarking.
Based on these results, we demonstrate that LLMS can generate new metaheuristic algorithms which advance the Pareto frontier of nonconvex optimization methods, as measured by log relative error and elapsed compute time.
We demonstrate that using an evolutionary approach similar to that in AlphaEvolve creates a statistically significant improvement in performance, though this appears to be dependent on the language model.
We plan on extending this work to gradient-based optimization methods, in order to be able to take advantage of tools like pytorch autograd and to benefit work on optimizers used in language models.